P4694 [PA2013] Raper

P4694 [PA2013] Raper

其实就是 CF802O 。但是这里用模拟费用流理解这个过程。

第一步仍然是 wqs 二分。

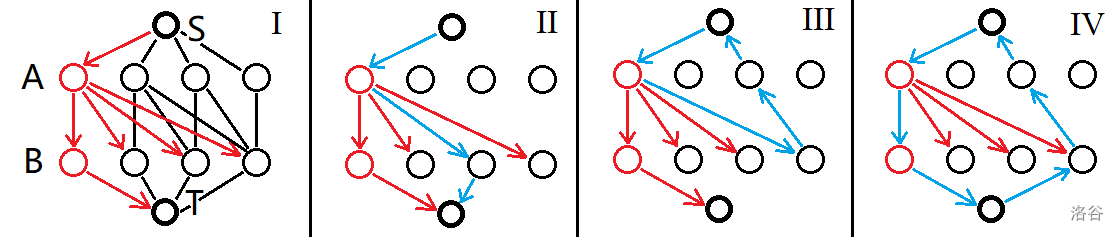
在情况 II 中，即选择可用的最小的。

在情况 III 中，替换一个更大的。

在情况 IV 中，$T\to S$ 的权值小于 $0$ 才选择，因此将其退流并不优。

于是可以得到和反悔贪心一样的代码了。

查看代码

#include <cstdio>
#include <queue>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 5e5 + 10;
LL ans;
int n, m, cnt, A[N], B[N];
void check(LL x)
{
    cnt = ans = 0;
    priority_queue<PLI, vector<PLI>, greater<PLI>> q;
    for (int i = 1; i <= n; i++)
    {
        q.push(make_pair(A[i] - x, 1));
        PLI t = q.top();
        if (B[i] + t.first >= 0)
            continue;
        q.pop();
        cnt += t.second;
        ans += B[i] + t.first;
        q.push(make_pair(-B[i], 0));
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &A[i]);
    for (int i = 1; i <= n; i++)
        scanf("%d", &B[i]);
    LL l = 0, r = 2e9, res;
    while (l <= r)
    {
        LL mid = l + r >> 1;
        check(mid);
        cnt <= m ? (res = ans + (LL)mid * m, l = mid + 1) : r = mid - 1;
    }
    printf("%lld", res);
    return 0;
}

另有线段树模拟费用流（或者叫线段树加速贪心）的做法。